
連載一覧
- 入門 Keras (1) Windows に Tensorflow と Keras をセットアップ
- 入門 Keras (2) パーセプトロンとロジスティック回帰
- 入門 Keras (3) 線形分離と多層パーセプトロン
第3回は、前回第2回の最後で行った XOR 回路の学習について考えます。
線形分離とは
OR や XOR の2つの入力を X 軸 Y 軸として2次元のグラフとして表示してみます。青の ● 印が出力 Y=0 で、オレンジが Y=1 です。回路が出力することを 0 または 1 に分類すると考えますと OR 回路の方はその領域を1本の直線を使って分類することが出来るのに対して XOR は1本の直線では分けることが出来ません。2本が必要になります。
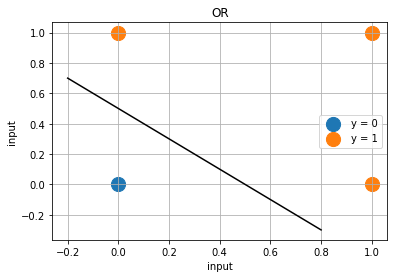
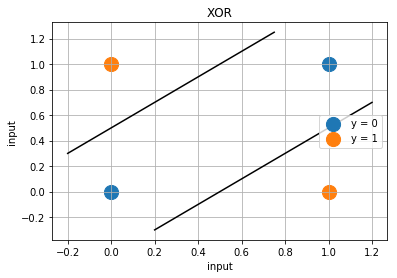
OR のように1本の線で分離可能な問題を 線形分離可能な問題 といい、XOR のように線形分離出来ない問題を 線形分離不可能な問題 と言います。また線形分離可能な問題を解くことの出来る機械を 線形分類器 (linear classifier) と言います。
単純パーセプトロンやロジスティック回帰は線形分類器であって、そのままでは XOR のように線形分離不可能なものを学習することが出来ません。といっても XOR のように単純なものも学習させることが出来ないのは困ります。上手く学習出来るようにするにはどのようにすればよいでしょうか?
論理ゲートの有名な特性「NAND や NOR だけで他の全てのゲートを構成可能」を思い出してみましょう。同様に XOR は AND, OR, NOT ゲートだけ を使って構成することが出来ます。
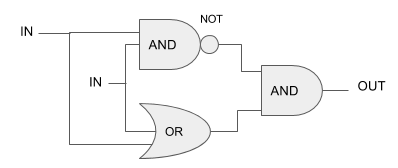
線形分離不可能な XOR 回路自体が、線形分離可能な OR, AND, NOT で書き換えることが出来るということは、 線形分類器も複数組み合わせれば 上手く分類できるかもしれません。やってみましょう。第2回で使った単純パーセプトロンのネットワークは出力層の一層だけでしたが、中間層を以下のように追加します。各ニューロンからの出力は一つとしていますので、追加した中間層は次の出力層のために二つ出力させる必要があるため、ニューロンが2個必要になります。
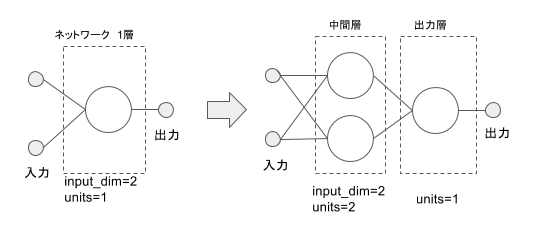
多層パーセプトロン
基本的には単純パーセプトロンと同じですが、それを多数層状に積み重ねたものを 多層パーセプトロン と言います。第2回で構成したようにモデルを作成してみます。Sequential モデルで、上の図のように2つの層で構成します。最初の中間層は入力の input_dim =2 で出力の数でもあるユニット数は units = 2 になります。後ろの出力層は入力が2でユニットが1になりますが。前の層の出力数は既に決まっていますので input_dim の記述は省略できます。
model = Sequential()
model.add(Dense(input_dim=2, units=2)) # 中間層
model.add(Activation('sigmoid'))
model.add(Dense(units=1)) # 出力層
model.add(Activation('sigmoid'))
他の部分は前回の記事で試したのと同じものを使い以下になります。エポック数は大幅に増やして 1000 以上に増やしています。
# モジュール読み込み
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import SGD
# 乱数を固定値で初期化
np.random.seed(0)
# シグモイドの単純パーセプトロン作成
model = Sequential()
model.add(Dense(input_dim=2, units=2)) # 中間層
model.add(Activation('sigmoid'))
model.add(Dense(units=1)) # 出力層
model.add(Activation('sigmoid'))
model.compile(loss='binary_crossentropy', optimizer=SGD(lr=0.1))
# トレーニング用入力 X と正解データ T
X = np.array( [[0,0],
[0,1],
[1,0],
[1,1]] )
T = np.array( [[0],
[1],
[1],
[0]] )
# トレーニング
model.fit(X, T, epochs=1000, batch_size=1)
# トレーニングの入力を流用して実際に分類
Y = model.predict_classes(X, batch_size=1)
print()
print("TEST")
print(Y == T)
Using TensorFlow backend. Epoch 1/1000 4/4 [==============================] - 2s - loss: 0.7600 Epoch 2/1000 4/4 [==============================] - 0s - loss: 0.7471 Epoch 3/1000 4/4 [==============================] - 0s - loss: 0.7375 : : : : : : : : : : : : 4/4 [==============================] - 0s - loss: 0.0827 Epoch 999/1000 4/4 [==============================] - 0s - loss: 0.0824 Epoch 1000/1000 4/4 [==============================] - 0s - loss: 0.0822 1/4 [======>.......................] - ETA: 0s TEST [[ True] [ True] [ True] [ True]]
上の例のようにおおよそ 1000 回のエポックが必要でしたが、単純パーセプトロンを2層、計3個のニューロン使ったことで線形分離不可能な XOR を学習することが出来ました!
このようにハイパーパラメーターのチューニングや様々な手法を組み合わせながら、 ネットワークの層を追加していくことで高い能力を発揮する のがディープラーニングの基本的な仕組みであり、 ディープ と名がつく由来になっています。
次回は来年1月9日(火)に 「多クラス分類 – Iris データを学習する」 をお届けする予定です! ここまでは2値分類に絞っていましたが、実践的なディープラーニングでは必須となる「多値への分類」について解説する予定です。ご期待ください。



