主要なゲームエンジンでも、例えばUnityのHDRPやUE5がそうですが、物理的なライト設定や露光調整が出来るようになっております。


しかし、所詮コンピューターグラフィックスだから、どの程度現実なんだ!とか、数値の精度は大丈夫なのか!とか、色々気になるところがあるような気がします。そもそもカメラにとって、この数値はどういう意味なのでしょうか?
というわけで、光源と露光について、現実の設定で描画を構築したらまともな階調の絵面がつくれるのかどうか……つまり、コンピューターグラフィックスにもっともらしい晴れの日の太陽光源の数値を入力すると、最終的にカメラのEVが15,16程度で妥当な見栄えが得られるのかどうかを導出してみましょう。カメラに理解のある方であればこの辺の話はしっくりくると思いますが、現実のカメラでも大体晴れの日はEV15,16程度で撮影すると思います。
(とはいったものの、私自身はカメラの完全な素人で、スマホ以外保有もしておらず実際の知識はないです。そんな私みたいな人も、一応数式だけで理解できるものだということです。)
基礎(読み飛ばしてもいいです)
もしご存じなければ、輝度(luminance)と照度(illuminance)を理解するところからスタートです。
まず、輝度の定義を理解しましょう。輝度LはdI/dScosΘ(lm/(sr・m^2))と定義されます。Iは光度(lm/sr)です。はい、残念ですが光度も理解しましょう。
光度はI=dΦ/dωと定義されます。(物理も極限操作なんでしょうが、素朴な微小値として見做しても大丈夫です。)ここでωは立体角(sr)、Φは光束(lm)です。光束は波長の関数としての放射束と、視感度(人の目が刺激される度合い)との積を、全波長について積分したものです。内積です。波長ごとに放射束に比例しているようなものだという認識は持ちやすいでしょう。実際、放射束と対応しているという風に書かれることがあります。ですがあくまで心理的な値、心理物理量です。(つまり光束を内包するものもすべて心理的な値です。輝度も、照度も心理的です。)
また、立体角があるという事はすなわち、これはある位置から方向的には球状に(均一ではないが)放射されることを前提にした光束であることを想定しているということを示します。ある微小立体角に放射される光束の総量は一定であることから、距離によって光度は変化はしないことがわかります。
光度はつまり、単に微小立体角方向に発射される(微小)光束(光源から放射される放射束に、波長ごとに感度と比例した感覚値)です。そして輝度は同様に、(光度の)光束が発射されてくる光源のその微小面積あたりの光度だということです。輝度も光度の性質を引き継ぎ、距離によって変化しないことも分かるでしょう。
次に、照度(lm/m^2)です。定義はE=dΦ/dΣです。
ここでΣは照度の関心となる、光束Φが入射する面積です。輝度は光束の発射側の光源についての値でしたが、照度は光束を受ける側の値であることに注意しましょう。dΣが固定される時、光源から受ける光束は受ける面の角度によって変化します。
さて、照度Eには光度と輝度との関係式があります。
まず光度との関係が、Θを光を受ける面の法線と光源との角度とすると、微小立体角がdω=dΣcosΘ/r^2であることと、光度がI=dΦ/dωであることよりdΦ=IdΣcosΘ/r^2 が求まり、これを変形するとE=dΦ/dΣ=IcosΘ/r^2 となります。
これは、光度がある微小点を中心に広がる光束を表すコンセプトdΦ/dωであることを認識しておくと、あくまでこの式はある光を放つ微小点から、面積あたりに受ける光束だということが分かります。
また、輝度との関係が、(二つのΘが登場するため区別をつけまして)Θdstを光を受ける微小面の法線と光の方向のなす角度、Θsrcを光源の法線と、光源と光を受ける微小面の方向とのなす角度とすると、先ほどのE=dΦ/dΣ=IcosΘ/r^2を微小なものととらえdE=dIcosΘdst/r^2とし、またL=dI/(dScosΘsrc)よりdI=LdScosΘsrcであるからdE=(LdScosΘsrccosΘdst/r^2)が求まり、これを関与するS全体の積分とするとE=∫dE=∫(LcosΘsrccosΘdst/r^2)dSとなります。
一見複雑なのですが、すなわち全ての可視光源の面からやってくる輝度を、実際のその光源の見かけの面積に応じた量にして、面でうけとるというような読み取りができると思います。
また、この輝度の関係式は、更に∫cosΘdst/r^2dIと変形できますが、光度による照度を関心の範囲で拾い集めた式ということです。輝度との関係と光度との関係の式は、それぞれ視点が違うという事ですね。
サクっとした解説になるつもりだったので、図もなにも用意しませんでしたが、思ったより長い話になってしまいました。ドンマイ。
EV値の導出
では気を取り直して。早速導出です。今回は日中の環境を数値的に与えたら、EV値は本当に15から16あたりになるかどうかがテーマですが、そもそもEV値とはいったい何でしょうか。カメラを使う方にとっては、露光の基準的な感じで使われる値だと思いますが、厳密には二つ、以下のような定義があります。
・EV=log2(N^2/t) ここでtはシャッタースピード、NはF値
・EV=log2(LS/K) Lは輝度、SはISO感度、Kは校正定数
二つ目の式が、いやそのLはなんなんだよと、若干飛躍的に感じる訳ですが、EVの英Wikipedia(https://en.wikipedia.org/wiki/Exposure_value )に「”Correct” exposure is obtained when the f-number and exposure time match those “recommended” for given lighting conditions and ISO speed」とある通りいい感じの露光を得るために都合をつけたものだという感じがします。つまり、あるEV値を示すカメラの状態を入力したときに得られたLは”おすすめ”のコンディションなのでしょう。
ところで、ISO 12232あたりを参照すると代表的なライトに照らされた18%反射率(おそらく完全拡散反射)が階調の中心に来るようなものが平均的な露光だ、みたいなことが書いてあります。とりあえず、代表的なライトに照らされた18%完全拡散反射率の物体が返す輝度をLとして強引に与えれば、それを中心に”いい感じ”になってくれるということは暗に読み取れる気がします。とりあえずやってみましょう。
晴天の日中はhttp://photon.sci-museum.kita.osaka.jp/publish/text/koyomi/66.html様より、100,000ルクス(太陽光に対して垂直な面が受ける照度)ということです。これを定理的に信じます。

すると、上記のように正規化されたランバート拡散反射で、太陽の照度から輝度を取得することができます。ここから、更にEV値を求めていきます。
さて、EV値の二つ目の式にはISO感度というやつが入っています。一つ目の式の方がカメラプロパティ感満載という感じですが、ISO感度はセンサーの光をどの程度増幅させるかというような値なので、Lにくっついているのが自然なのでしょう。
現実のカメラでは、tを変更したり、ISOを合わせて狙いのEV値にしていくかもしれません。ただ、ISO感度を増やすとノイズが増える可能性があるので、理想的にはISOは100にしたいというような話が散見されます。よって、式に都合をつけ、EVについてISOが100だったらどういう値になるかを求めてみます。具体的には以下のようになります。
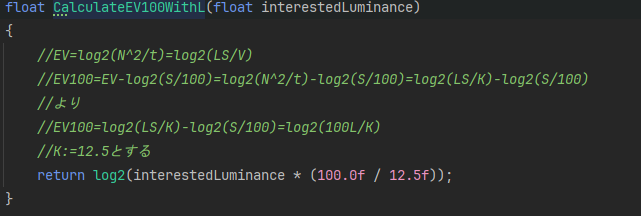
これでISO感度100の時のEV値が求まるわけです。
実際、100000luxの環境下でこの式log2(0.18 * 100000 * 1/π * (100 / 12.5))によって得られたEV値は、なんということでしょう
約 15.48
となりました。日中の妥当なEV値のような感触です!
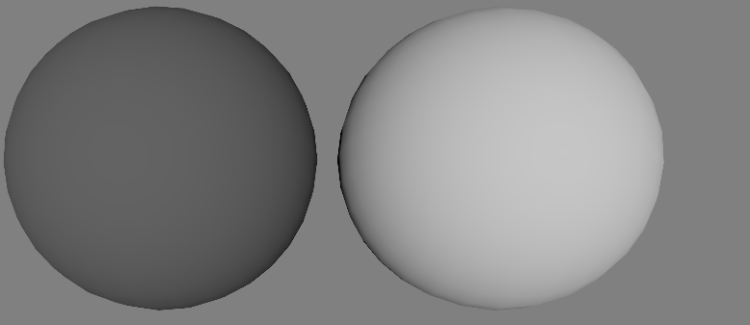
実際にGGXをつかって、roughness=0の非金属物体をsRGB環境で描画し、カメラ側から100000luxの伝統的Directional Lightを当て、得られたEV値で描写した様子です。右が反射率100%(白)で、左が反射率18%の物体です。環境光など他の光源は一切存在しません。
最後に
コンピューターグラフィックスでも、カメラについての露光や光源の設定は厳密だという事ですね。カメラの知識がないとダメですね。僕もカメラを買わないといけないな…
ライティング関連について、リアルタイムレンダリングに特有の不自然さがあるとすると、主には寧ろ光源そのものの実現からくるということでしょう。例えば現実では様々な散乱が発生し、環境全体が光源となりますが、リアルタイムレンダリングではそれを実現するために様々な苦労をしていて、結局不完全でありますからね。
★インフィニットループでは3Dゲーム開発にも取り組んでおります。興味がある方は是非採用情報をご確認ください。★